統計データを読み解く際、私たちは「平均値」を重要な指標として扱います。
しかし、一部に極端な値が存在する場合、平均値は必ずしも全体の実態を正確に表しません。
この現象はSNSで「校長現象」という名前で一時広まりました。
正式な統計学の名称ではないのですが、由来と意味を知るとなかなか理解しやすいです。
なぜこの名称が付いたのか、そしてこの現象が示唆する統計の特性について考察します。
「校長現象」の定義と由来
「校長現象」という名称は、「かつてたった1人の校長が1万人以上の女性と倫理的によくないことをしたせいで、全国の校長の平均◯◯人数が1〜2人になってしまう」という思考実験に由来しているといわれています。
このことを説明するのに、校長先生の給与の違いで解説しているものもありますが、学校の教職員と校長の給与体で説明するとわかりやすいです。
一般的な教職員の給与に比べ、校長職の給与が突出して高いことから、平均値が実態とかけ離れてしまっています。
例えば、ある学校で9人の教職員の月給が30万円、校長1人の月給が100万円だとします。この場合の平均値は37万円となりますが、実際には10人中9人が30万円であり、37万円という数字は現場の実態を正確に表していません。
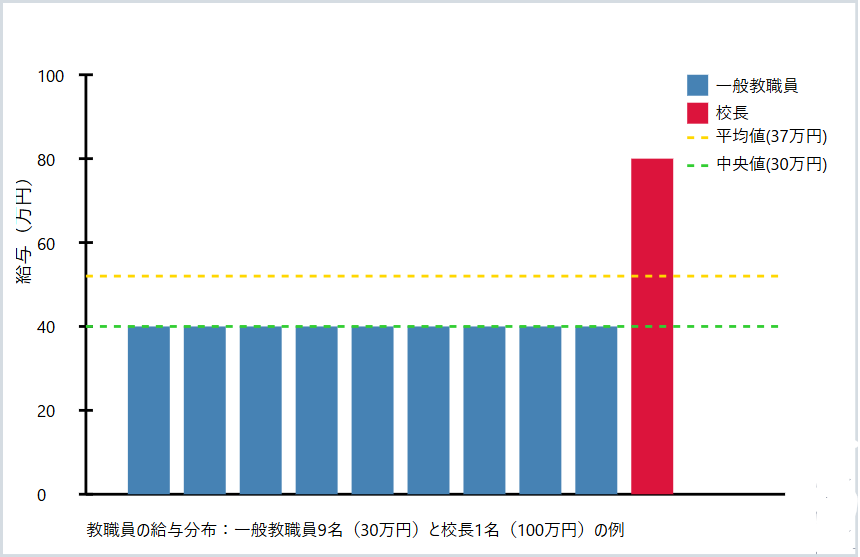
この現象は、データの分布が非対称で、一部に極端に高い値(または低い値)が存在する場合に発生します。統計学では、このような極端な値を「外れ値」と呼びます。
真面目に解説すると以上のようなことになります。
このことを説明するには、「大谷現象」という言葉の方が良いという意見もあります。
統計における平均値の特性
平均値は最も一般的な統計指標の一つですが、その性質上、外れ値の影響を強く受けます。
算術平均は、全てのデータの合計を標本数で割って求められますが、この計算方法ゆえに、極端な値が存在すると大きく歪められてしまいます。
この特性は、時として社会の実態を見えにくくする要因となります。
例えば、ある地域の世帯所得を考えた場合、一部の超富裕層の存在により、平均所得が一般的な世帯の実態よりもはるかに高く算出されることがあります。
下のポストは、東京は富裕層の集中で平均収入が高く見えるが、一般世帯の収入を表す中央値は低く、高物価のため実質的な生活水準は他県より厳しいということを伝えています。
中央値が有効な場合
このような場合、中央値の活用が有効です。中央値は、全データを順番に並べた際の中央に位置する値を指します。外れ値の影響を受けにくい特徴があり、多くの場合、実態をより正確に反映します。
先ほどの教職員の例では、中央値は30万円となり、現場の実態により即した数値となります。このように、平均値と中央値を比較することで、データの偏りや特徴をより深く理解することができます。
社会における「校長現象」の具体例
「校長現象」といわれる中央値と平均値の乖離は、様々な場面で観察されます。以下に代表的な例を挙げてみましょう。
- 企業規模の分布:少数の大企業と多数の中小企業が存在する状況
- SNSのフォロワー数:一部の人気アカウントと一般ユーザーの差
- 動画視聴回数:viral動画と一般的な動画の格差
- 不動産価格:都心部と郊外の価格差
これらの例では、いずれも平均値が実態を正確に表さない可能性が高く、複数の統計指標を用いた分析が必要となります。
データ解釈における留意点
統計データを解釈する際は、以下の点に留意する必要があります。
- 単一指標への依存を避ける
- データの分布を確認する
- 外れ値の存在とその影響を考慮する
- 目的に応じた適切な指標を選択する
特に、政策立案や経営判断において統計データを活用する場合、「校長現象」の存在を意識することで、より適切な判断が可能となります。
まとめ
「校長現象」という正式な名称があるわけではなく、これは一時的にSNSで話題になったにすぎません。
しかしこの現象の理解は、単なる統計の知識以上の意味を持ちます。それは、データの背後にある社会の構造や不均衡を読み解く視点を提供してくれるのです。
現代社会において、統計データは意思決定の重要な基礎となっています。
複数の統計指標を適切に組み合わせ、多角的な視点でデータを解釈する能力は、ますます重要性を増しています。
このようなことがあることを「校長現象」という名前で理解することは、1つの方法として理解できます。
統計は時として私たちの直感に反する結果を示します。しかし、その「ずれ」の中にこそ、重要な社会の真実が隠されているのかもしれません。データを読み解く際は、常にこの点を意識しておきたいものです。


